😂 Thanks for the chuckle -- though also... I'd read that I think
Sparrow_1029
For fuck's sake just name him

Wordle 1,343 5/6
⬜⬜⬜⬜🟨
🟩🟩🟩⬜⬜
🟩🟩🟩⬜🟩
🟩🟩🟩⬜🟩
🟩🟩🟩🟩🟩
Using Voyager App on Android, it appears that the syntax highlighting defaults to SQL for code blocks without a specified language?
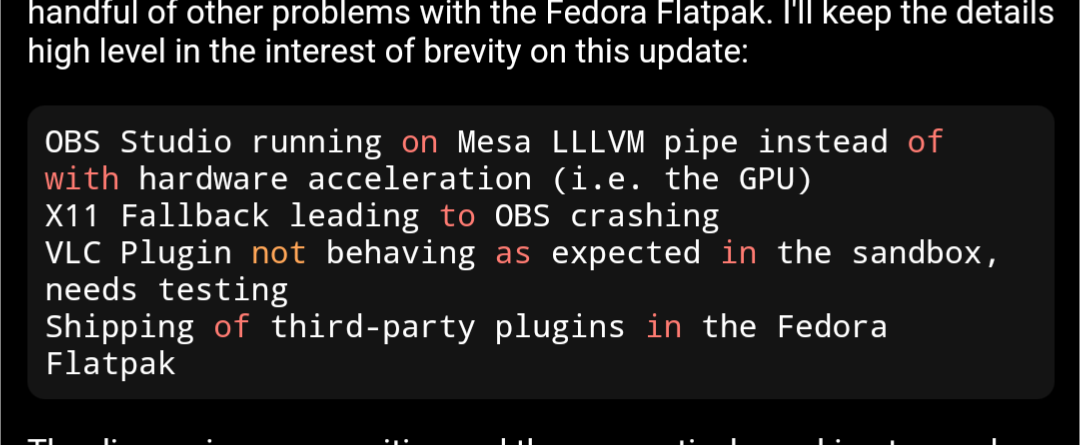
Strange
Went climbing at the gym, went snowboarding, working on setting up the *arr stack + kodi on a raspi5 for a friend. I'm curious to see how well it performs with downloading and serving video content. Getting a (pretty old, well-used creality) 3d printer out of it... new hobby??
I've heard this from other educators as well! What do you think the ramifications are down the line with people knowing less and less about how computers actually function?
I mean, I guess mechanics have jobs because most people know how to use a gas pedal and steering wheel, but not how an internal combustion engine works?
Weirdest one for me yet
Wordle 1,338 6/6
🟩⬜🟩⬜🟩
🟩⬜🟩⬜🟩
🟩⬜🟩⬜🟩
🟩⬜🟩⬜🟩
🟩⬜🟩⬜🟩
🟩🟩🟩🟩🟩
Wordle 1,334 3/6
⬜⬜⬜⬜⬜
⬜🟨⬜🟨🟩
🟩🟩🟩🟩🟩
Connections Puzzle #611
🟨🟨🟨🟨
🟩🟩🟩🟩
🟪🟪🟪🟪
🟦🟦🟦🟦
Skill 95/99
1 in 28 uniqueness
In three!
Wordle 1,331 3/6
⬜⬜⬜🟨⬜
🟨🟩🟨🟨⬜
🟩🟩🟩🟩🟩
Which faith? Why doesn't the announcement declare that all faiths will be equally represented and defended? Why is she a christian pastor? What.The. FUCK. Happened to separation of church and state?


*looks at wallet
*looks at steam deck
*squints eyes at wallet
...
Still wondering if and when is the right time to buy one. I may be in the market for a new personal laptop (non-gaming) first before I can consider getting a deck. C'est la vie