this post was submitted on 01 Dec 2023
48 points (98.0% liked)
Learn Programming
1713 readers
1 users here now
Posting Etiquette
-
Ask the main part of your question in the title. This should be concise but informative.
-
Provide everything up front. Don't make people fish for more details in the comments. Provide background information and examples.
-
Be present for follow up questions. Don't ask for help and run away. Stick around to answer questions and provide more details.
-
Ask about the problem you're trying to solve. Don't focus too much on debugging your exact solution, as you may be going down the wrong path. Include as much information as you can about what you ultimately are trying to achieve. See more on this here: https://xyproblem.info/
Icon base by Delapouite under CC BY 3.0 with modifications to add a gradient
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
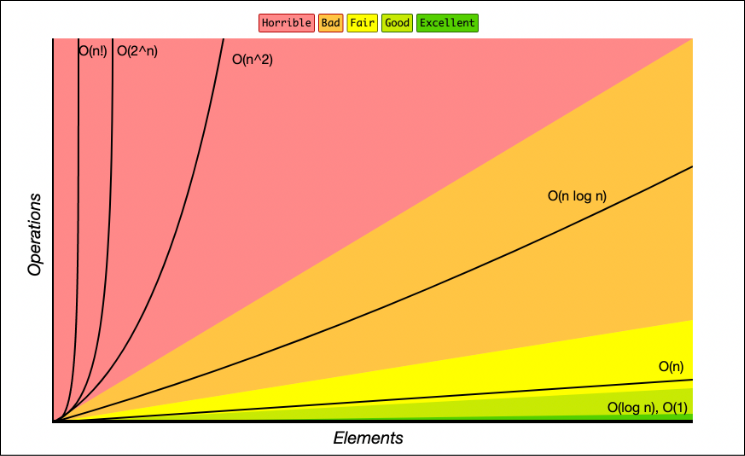
I don't agree that it's useless or misguiding. The smaller dataset, the less important it is, but it makes massive difference how the rest of the algorithm will be working and changing context around it.
Let's say that you need to sort 64 ints, in a code that starts our operating system. You need to sort it once per boot, and you boot less frequently than once per day, in fact you know instances of the OS that have 14 years of uptime, so it doesn't matter at all right? Welp. Now your OS is used by a big cloud provider and they use that code to boot the kernel 13 billions times per day. The context changed, time passed by, your silly bubble sort that doesn't matter on small numbers is still there.
While I get your point, you're still slightly misguided.
Sometimes for a smaller dataset an algorithm with worse asymptomatic complexity can be faster.
Some examples:
Big O notation only considers the largest factor. It is still important to consider the lower order factors in some cases. Assume the theoretical time complexity for an algorithm A is 2nlog(n) + 999999999n and for algorithm B it is n^2 + 7n. Clearly with a small n, B will always be faster, even though B is O(n^2) and A is O(nlog(n)).
Sorting is actually a great example to show how you should always consider what your data looks like before deciding which algorithm to use, which is one of the biggest takeaways I had from my data structures & algorithms class.
This youtube channel also has a fairly nice three-part series on the topic of sorting algorithms: https://youtu.be/_KhZ7F-jOlI?si=7o0Ub7bn8Y9g1fDx
Except the point of this post is that a different sort with worse Big O could be faster with a small dataset.
The fact that you're sorting those 64 ints billions of times simply doesn't matter. The "slower" sort is still faster in practice.
That's why it's important to realize that Big O notation can be useless for small datasets. Because it can actually just be lying to you.
It's actually mathematical. Take any equation:
y = x^2 + xFor large x the squared term dominates. The linear may as well not exists. It's O(x^2). But when x is below 1? Well suddenly that linear term is the more important one! Below 1 it's actually O(x) in practice.