Funny idea, but good luck getting this leaky bucket from the Baltic sea all the way via Gibraltar to the Black sea.
Gobbel2000
Nah, this photo is definitely not from this year.
Pretty sure that's correct. You can also see the elevated U2 in the background.
"Fraunce" is my favorite part of this map.
Rust
Nice ending for this year. Lock and key arrays are just added together and all elements must be <= 5. Merry Christmas!
Solution
fn flatten_block(block: Vec<Vec<bool>>) -> [u8; 5] {
let mut flat = [0; 5];
for row in &block[1..=5] {
for x in 0..5 {
if row[x] {
flat[x] += 1;
}
}
}
flat
}
fn parse(input: &str) -> (Vec<[u8; 5]>, Vec<[u8; 5]>) {
let mut locks = Vec::new();
let mut keys = Vec::new();
for block_s in input.split("\n\n") {
let block: Vec<Vec<bool>> = block_s
.lines()
.map(|l| l.bytes().map(|b| b == b'#').collect::<Vec<bool>>())
.collect();
assert_eq!(block.len(), 7);
// Lock
if block[0].iter().all(|e| *e) {
locks.push(flatten_block(block));
} else {
keys.push(flatten_block(block));
}
}
(locks, keys)
}
fn part1(input: String) {
let (locks, keys) = parse(&input);
let mut count = 0u32;
for l in locks {
for k in &keys {
if l.iter().zip(k).map(|(li, ki)| li + ki).all(|sum| sum <= 5) {
count += 1;
}
}
}
println!("{count}");
}
fn part2(_input: String) {
println!("⭐");
}
util::aoc_main!();
Also on github
Rust + Pen and Paper
Yikers. Part 2 took a while, staring at this diagram for hours. Eventually I noticed that each of these blocks has two pairs of (XOR, AND) gates sharing the same inputs (and inputs aren't changed). So I matched up these pairs based on a distance metric of how much needs to be swapped to fit together. This helped me identify 4 blocks with errors, the rest was solved using pen and paper (one block is missing as it became apparent at that point):
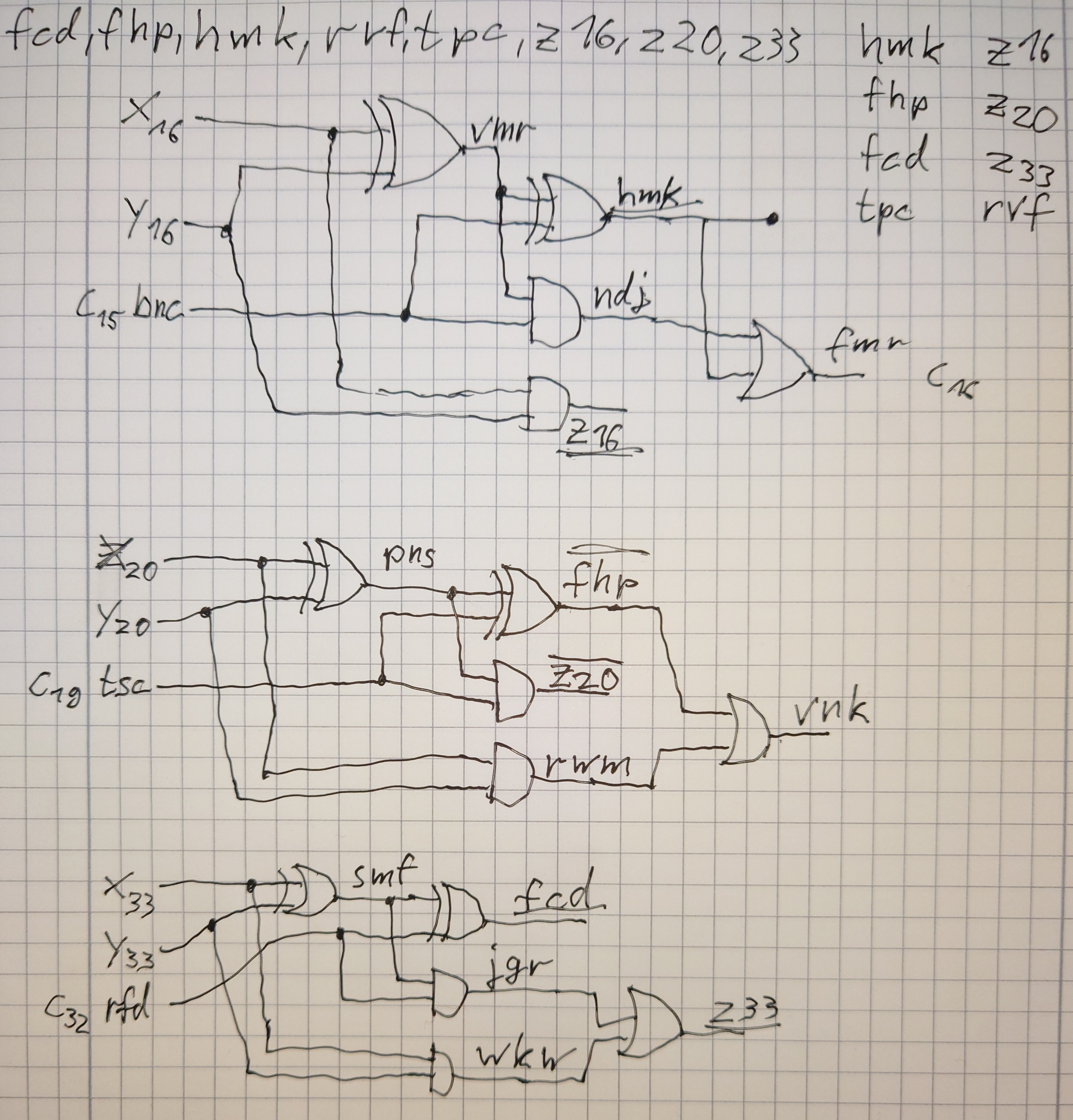
There is also some code, but do yourself and me a favor and don't look at it. While it does turn up the correct solution, it probably won't with any other input, especially not the examples.
Rust
Finding cliques in a graph, which is actually NP-comlete. For part two I did look up how to do it and implemented the Bron-Kerbosch algorithm. Adding the pivoting optimization improved the runtime from 134ms to 7.4ms, so that is definitely worth it (in some sense, of course I already had the correct answer without pivoting).
Solution
use rustc_hash::{FxHashMap, FxHashSet};
fn parse(input: &str) -> (Vec<Vec<usize>>, FxHashMap<&str, usize>) {
let mut graph = Vec::new();
let mut names: FxHashMap<&str, usize> = FxHashMap::default();
for l in input.lines() {
let (vs, ws) = l.split_once('-').unwrap();
let v = *names.entry(vs).or_insert_with(|| {
graph.push(vec![]);
graph.len() - 1
});
let w = *names.entry(ws).or_insert_with(|| {
graph.push(vec![]);
graph.len() - 1
});
graph[v].push(w);
graph[w].push(v);
}
(graph, names)
}
fn part1(input: String) {
let (graph, names) = parse(&input);
let mut triples: FxHashSet<[usize; 3]> = FxHashSet::default();
for (_, &v) in names.iter().filter(|(name, _)| name.starts_with('t')) {
for (i, &u) in graph[v].iter().enumerate().skip(1) {
for w in graph[v].iter().take(i) {
if graph[u].contains(w) {
let mut triple = [u, v, *w];
triple.sort();
triples.insert(triple);
}
}
}
}
println!("{}", triples.len());
}
// Bron-Kerbosch algorithm for finding all maximal cliques in a graph
fn bron_kerbosch(
graph: &[Vec<usize>],
r: &mut Vec<usize>,
mut p: FxHashSet<usize>,
mut x: FxHashSet<usize>,
) -> Vec<Vec<usize>> {
if p.is_empty() && x.is_empty() {
return vec![r.to_vec()];
}
let mut maximal_cliques = Vec::new();
let Some(&u) = p.iter().next() else {
return maximal_cliques;
};
let mut p_pivot = p.clone();
for w in &graph[u] {
p_pivot.remove(w);
}
for v in p_pivot {
let pn = graph[v].iter().filter(|w| p.contains(w)).copied().collect();
let xn = graph[v].iter().filter(|w| x.contains(w)).copied().collect();
r.push(v);
let new_cliques = bron_kerbosch(graph, r, pn, xn);
r.pop();
maximal_cliques.extend(new_cliques);
p.remove(&v);
x.insert(v);
}
maximal_cliques
}
fn part2(input: String) {
let (graph, names) = parse(&input);
let p = (0..graph.len()).collect();
let mut r = Vec::new();
let maximal_cliques = bron_kerbosch(&graph, &mut r, p, FxHashSet::default());
let maximum_clique = maximal_cliques
.iter()
.max_by_key(|clique| clique.len())
.unwrap();
let mut lan_names: Vec<&str> = names
.iter()
.filter(|(_, v)| maximum_clique.contains(v))
.map(|(name, _)| *name)
.collect();
lan_names.sort_unstable();
println!("{}", lan_names.join(","));
}
util::aoc_main!();
Also on github
Glad to be able to help. This one really was a doozy.
Rust
Nice breather today (still traumatized from the robots). At some point I thought you had to do some magic for predicting special properties of the pseudorandom function, but no, just collect all values, have a big table for all sequences and in the end take the maximum value in that table. Part 1 takes 6.7ms, part 2 19.2ms.
Solution
fn step(n: u32) -> u32 {
let a = (n ^ (n << 6)) % (1 << 24);
let b = a ^ (a >> 5);
(b ^ (b << 11)) % (1 << 24)
}
fn part1(input: String) {
let sum = input
.lines()
.map(|l| {
let n = l.parse().unwrap();
(0..2000).fold(n, |acc, _| step(acc)) as u64
})
// More than 2¹⁰ 24-bit numbers requires 35 bits
.sum::<u64>();
println!("{sum}");
}
const N_SEQUENCES: usize = 19usize.pow(4);
fn sequence_key(sequence: &[i8]) -> usize {
sequence
.iter()
.enumerate()
.map(|(i, x)| (x + 9) as usize * 19usize.pow(i as u32))
.sum()
}
fn part2(input: String) {
// Table for collecting the amount of bananas for every possible sequence
let mut table = vec![0; N_SEQUENCES];
// Mark the sequences we encountered in a round to ensure that only the first occurence is used
let mut seen = vec![false; N_SEQUENCES];
for l in input.lines() {
let n = l.parse().unwrap();
let (diffs, prices): (Vec<i8>, Vec<u8>) = (0..2000)
.scan(n, |acc, _| {
let next = step(*acc);
let diff = (next % 10) as i8 - (*acc % 10) as i8;
*acc = next;
Some((diff, (next % 10) as u8))
})
.unzip();
for (window, price) in diffs.windows(4).zip(prices.iter().skip(3)) {
let key = sequence_key(window);
if !seen[key] {
seen[key] = true;
table[key] += *price as u32;
}
}
// Reset seen sequences for next round
seen.fill(false);
}
let bananas = table.iter().max().unwrap();
println!("{bananas}");
}
util::aoc_main!();
Also on github
Rust
For me this was the hardest puzzle so far this year. First I did a bunch of things that turned out not to work properly. For example I tried to solve it with a greedy algorithm that always moved horizontally first then vertically, but that ignores the gaps that need to be avoided (what a sneaky requirement) and also somehow doesn't guarantee the shortest sequence.
After reaching part 2 it became clear that a recursive function (with memoization) is needed again, and of course in the end it turned out a lot simpler than what I had cooked up before (you don't want to see that). Now even part 2 takes just 1.6ms.
Solution
use euclid::{default::*, point2, vec2};
use rustc_hash::FxHashMap;
use std::iter;
type Move = Option<Vector2D<i32>>;
const KEYPAD_GAP: Point2D<i32> = point2(0, 3);
const DPAD_GAP: Point2D<i32> = point2(0, 0);
fn keypad_pos(n: u8) -> Point2D<i32> {
match n {
b'7' => point2(0, 0),
b'8' => point2(1, 0),
b'9' => point2(2, 0),
b'4' => point2(0, 1),
b'5' => point2(1, 1),
b'6' => point2(2, 1),
b'1' => point2(0, 2),
b'2' => point2(1, 2),
b'3' => point2(2, 2),
b'0' => point2(1, 3),
b'A' => point2(2, 3),
other => panic!("Invalid keypad symbol {other}"),
}
}
// `None` is used for A
fn dpad_pos(d: Move) -> Point2D<i32> {
match d {
Some(Vector2D { x: 0, y: -1, .. }) => point2(1, 0),
None => point2(2, 0),
Some(Vector2D { x: -1, y: 0, .. }) => point2(0, 1),
Some(Vector2D { x: 0, y: 1, .. }) => point2(1, 1),
Some(Vector2D { x: 1, y: 0, .. }) => point2(2, 1),
other => panic!("Invalid dpad symbol {other:?}"),
}
}
fn moves_for_diff(diff: Vector2D<i32>, pos: Point2D<i32>, gap: Point2D<i32>) -> Vec<Vec<Move>> {
let horizontal = iter::repeat_n(
Some(vec2(diff.x.signum(), 0)),
diff.x.unsigned_abs() as usize,
);
let vertical = iter::repeat_n(
Some(vec2(0, diff.y.signum())),
diff.y.unsigned_abs() as usize,
);
if pos + vec2(diff.x, 0) == gap {
// Must not move horizontal first, or we hit the gap
vec![vertical.chain(horizontal).chain(iter::once(None)).collect()]
} else if pos + vec2(0, diff.y) == gap {
vec![horizontal.chain(vertical).chain(iter::once(None)).collect()]
} else {
// Try both horizontal first and vertical first
vec![
horizontal
.clone()
.chain(vertical.clone())
.chain(iter::once(None))
.collect(),
vertical.chain(horizontal).chain(iter::once(None)).collect(),
]
}
}
fn dpad_sequence_len(
start: Move,
end: Move,
rounds: u32,
cache: &mut FxHashMap<(Move, Move, u32), u64>,
) -> u64 {
if rounds == 0 {
return 1;
}
if let Some(len) = cache.get(&(start, end, rounds)) {
return *len;
}
let start_pos = dpad_pos(start);
let end_pos = dpad_pos(end);
let diff = end_pos - start_pos;
let possible_paths = moves_for_diff(diff, start_pos, DPAD_GAP);
let shortest_sequence = possible_paths
.iter()
.map(|moves| {
moves
.iter()
.fold((0, None), |(cost, prev), &m| {
(cost + dpad_sequence_len(prev, m, rounds - 1, cache), m)
})
.0
})
.min()
.unwrap();
cache.insert((start, end, rounds), shortest_sequence);
shortest_sequence
}
fn keypad_sequence_len(start: u8, end: u8, rounds: u32) -> u64 {
let start_pos = keypad_pos(start);
let end_pos = keypad_pos(end);
let diff = end_pos - start_pos;
let possible_paths = moves_for_diff(diff, start_pos, KEYPAD_GAP);
let mut cache = FxHashMap::default();
possible_paths
.iter()
.map(|moves| {
moves
.iter()
.fold((0, None), |(cost, prev), &m| {
(cost + dpad_sequence_len(prev, m, rounds, &mut cache), m)
})
.0
})
.min()
.unwrap()
}
fn solve(input: &str, rounds: u32) -> u64 {
let mut sum: u64 = 0;
for l in input.lines() {
let mut prev = b'A';
let mut len = 0;
for b in l.bytes() {
len += keypad_sequence_len(prev, b, rounds);
prev = b;
}
let code_n: u64 = l.strip_suffix('A').unwrap().parse().unwrap();
sum += code_n * len;
}
sum
}
fn part1(input: String) {
println!("{}", solve(&input, 2));
}
fn part2(input: String) {
println!("{}", solve(&input, 25));
}
util::aoc_main!();
Also on github
There is exactly one path without cheating, so yes, the distance to one end is always the total distance minus the distance to the other end.
Only if you convert rubles by "purchase power parity" as opposed to the market rate, which seems like a weird way to manipulate data to fit some narrative.