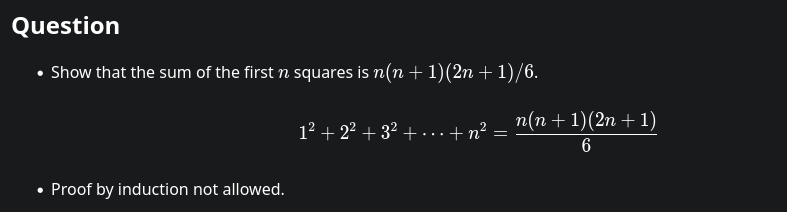solution
Used some Minecraft for visualization on this one. Assumes you already know how to sum constants and sequential integers.
When summing the odd integers 1 + 3 + 5 + ...,, they sum to the squares: The first n odd integers sum to n^2. This can be seen with a pretty simple construction, shown here - each additional layer, completing the next size square, has two more blocks than the previous one - they're the odd integers summed in sequence.
You can build a vaguely similar construction for the sum of squares - one quarter of a stepped pyramid, seen here. Seen from above in this view, it has the same structure as the sum of odds square on a per-layer basis. So each layer of the pyramid has an odd number of columns in it, in sequence, from 1 column for the highest layer to (2n-1) columns (the nth odd number) for the bottom layer. Each layer decreases in height by 1. So we can say that the 4th layer from the top, for example, has 7 columns in it (4th odd number), with n-3 blocks in each column (n in first layer, n-1 in second, n-2 in third, n-3 in fourth). So the columns in this layer have 7(n-3) blocks contained within them, total.
Going by this, we can write a sum to count the blocks.
Σ (i = 1 to n) n^2 = Σ (i = 1 to n) (2i-1) * (n-i+1)
The idea is we're counting up the blocks in all the columns that correspond to each distinct height. (2i-1) is giving us the i-th odd number, for the number of distinct columns at each level, while n-i+1 then gives us the number of blocks in each of those columns - and so their product counts the total blocks in all of those columns. All sums are from i = 1 to n, and that's omitted for less clutter. From here:
Σi^2 = Σ(2i-1) * (n-i+1)
Σi^2 = Σ(2in - 2i^2 + 3i - n - 1) → Expand, combine like terms
Σi^2 = (2n+3)Σi - 2Σi^2 - (n+1)Σ1 → Group by power of i, factor out constants
3Σi^2 = (2n+3)Σi - (n+1)Σ1 → Add 2Σi^2 to both sides
3Σi^2 = (2n+3)n(n+1)/2 - n(n+1) → Evaluate sums on right
3Σi^2 = ((2n+3)n(n+1) - 2n(n+1)) / 2 → Combine right to one fraction
3Σi^2 = n(n+1)(2n+1) / 2 → Factor n(n+1) from numerator, simplify
Σi^2 = n(n+1)(2n+1) / 6 → Divide both sides by 3, QED
Would like to mention I didn't view the hint, since I now see the hint mentions both constructions and Minecraft - the solution actually came to me before making it in Minecraft, but my attempts to explain it without images were pretty inadequate.
A second setup I also see, using the same stepped pyramid, is: Σ (i = 1 to n) (Σ (k = n - i + 1 to n) k). This one is summing up cross-sections of the pyramid perpendicular to the ground, from the light side of the pyramid to the heavy side. When i = n it's a full triangular cross-section (with 1 + 2 + 3 + ... + n blocks), but as you move across the pyramid, the top of the triangle (the side that starts at 1 block) gets cut off more and more - so when i = 1 it's just the bottom layer, with n blocks in it. This setup does also lead to a valid proof for the formula for Σi^2, if you work it out.