this post was submitted on 21 Sep 2023
1285 points (97.8% liked)
Memes
47099 readers
1004 users here now
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
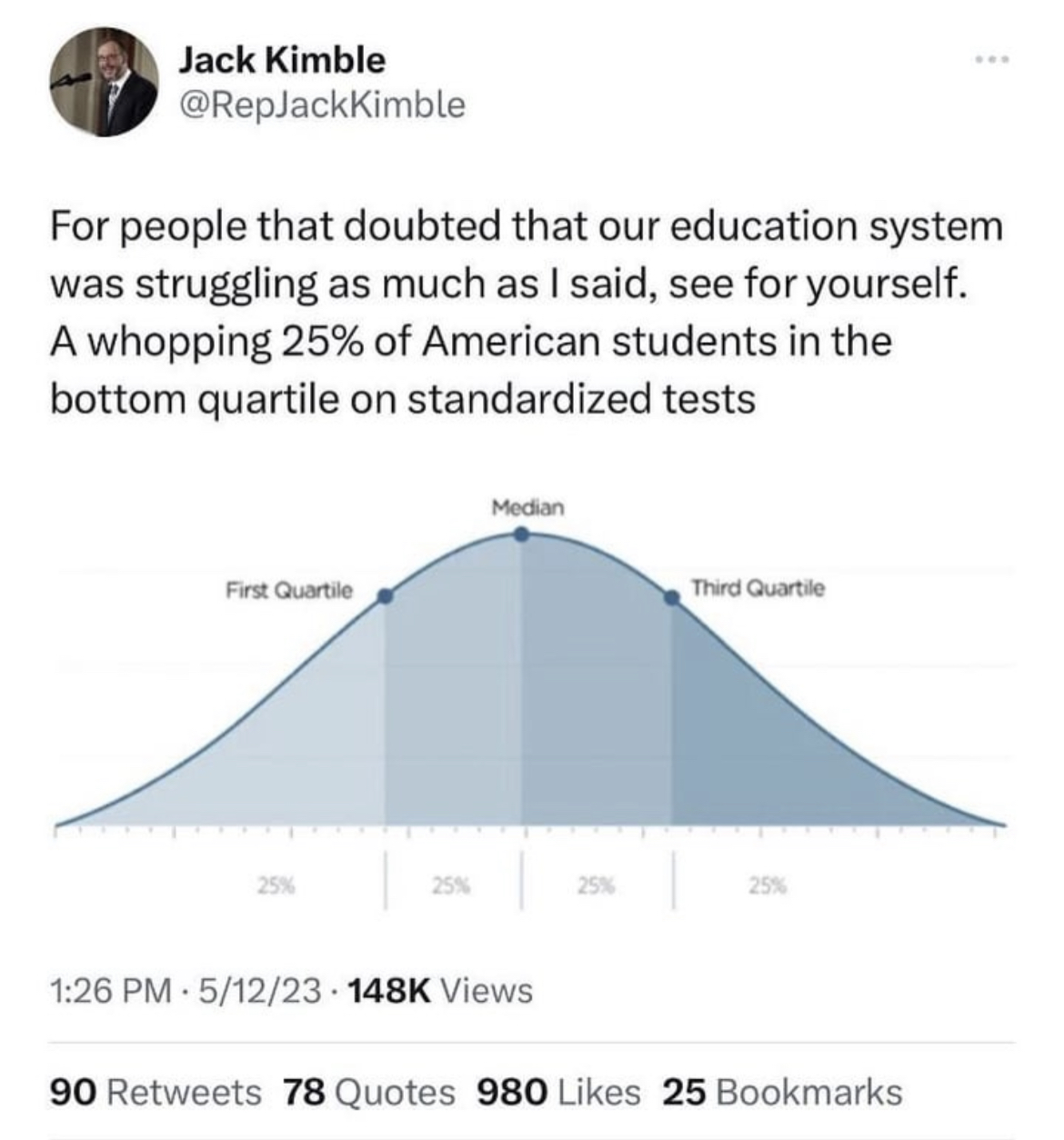
No, this is how a graph showing quartiles will always look because quartiles, by definition, always include a fixed percentage of the studied population under them.
In this case the lower quartile will always have 25% of the population under it, 50% under the second quartile, and 75% under the third quartile.
Quartiles break a population into 4 equal portions.
While that's true, the actual empirical curve does not have to be smooth. Or gaussian.
Spendrill is not misunderstanding the OP. He's just saying that if intelligence could be measured by a better metric, then distribution of that metric among the population would not look as smooth as the one in the OP.
Not if you're breaking the data into quartiles. Holy shit, do you really think the curve will be any different? Really? All that will happen is that some people will move around in the distribution. And the smoothing does not at all relate to how intelligence is measured but rather how it's reported - in this graph.
I think you’re talking past each other — you’re talking about the box plot and they’re talking about the histogram
Yes I think it's very possible that if you were to graph a population's Intelligence using a some empirical score, then it has a high probability to NOT look exactly like a normal distribution.
For example, let's say that there was some score called "intelligence score" that scores people's intelligence from 0-100. Do you think that if you were to graph a given population's "intelligence score" that it would be EXACTLY centered around 50 in a Normal distribution? I think that's unlikely. It's more likely that there would be local maximums or minimums, or various skews in the graph. There could be a small peak at score 75, or a trough at 85. There could be all sorts of distributions.
And guess what? Given this hypothetical distribution, you could STILL draw lines somewhere on the graph showing quartiles. Those lines might not be at 25-50-75. They might not even be the same distance apart from each other. But you CAN draw them somewhere to split the scores. Just because a graph "has quartiles" does not mean it will always look like the OP.
I know what this graph is, I was talking about a graph that actually showed something useful. If you've got a couple of hours to learn something useful then you could do worse than to look at this video: https://www.youtube.com/watch?v=UBc7qBS1Ujo