this post was submitted on 08 May 2024
17 points (90.5% liked)
Daily Maths Challenges
189 readers
1 users here now
Share your cool maths problems.
Complete a challenge:
- Post your solution in comments, if it is exactly the same as OP's solution, let us know.
- Have fun.
Post a challenge:
- Doesn't have to be original, as long as it is not a duplicate.
- Challenges not riddles, if the post is longer than 3 paragraphs, reconsider yourself.
- Optionally include solution in comments, let it be clear this is not a homework help forums.
- Tag [unsolved] if you don't have a solution yet.
- Please include images, if your question includes complex symbols, attach a render of the maths.
Feel free to contribute to a series by DMing the OP, or start your own challenge series.
founded 6 months ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments

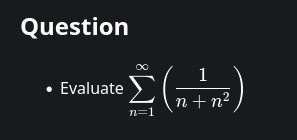
Since this is everyone's favorite example of telescoping sums, let's do it another way just for giggles.
Combinatorial proof
The denominator is P(n+1, 2) which is the number of ways for 2 specified horses to finish 1st and second in an n+1 horse race. So imagine you're racing against horses numbered {1, 2, 3, ....}. Either you win, which has probability 0 in the limit, or there is a lowest numbered horse, n, that finishes ahead of you. The probability that you beat horses {1,2, ... , n-1} but lose to n is (n-1)! / (n+1)! or P(n+1, 2) or 1/(n^2^+n), the nth term of the series. Summing these mutually exclusive cases exhausts all outcomes except the infinitesimal possibility that you win. Therefore the infinite sum is exactly 1.