this post was submitted on 07 Apr 2024
497 points (95.6% liked)
Security
5431 readers
1 users here now
Confidentiality Integrity Availability
founded 5 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
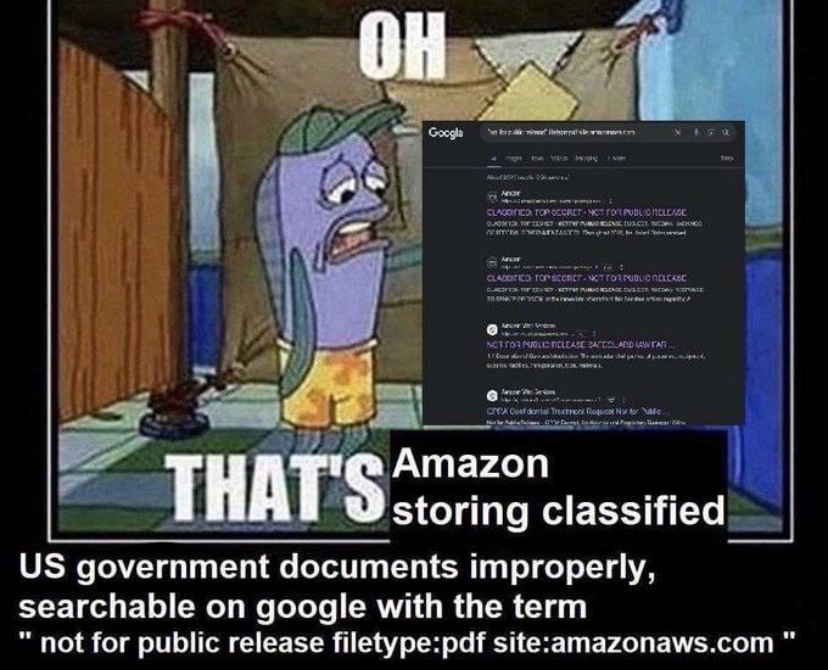
Compartmentalisation helps
If no one actually knows the plan other than the guy in charge, no one can leak the plan:
True, and interesting since this can be used as a statistical lever to ignore the exponential scaling effect of conditional probability, with a minor catch.
Lemma: Compartmentalization can reduce, even eliminate, chance of exposure introduced by conspirators.
Proof: First, we fix a mean probability p of success (avoiding accidental/deliberate exposure) by any privy to the plot.
Next, we fix some frequency k~1~, k~2~, ... , k~n~ of potential exposure events by each conspirators 1, ..., n over time t and express the mean frequency as k.
Then for n conspirators we can express the overall probability of success as
1 ⋅ p^tk~1~^ ⋅ p^tk~2~^ ⋅ ... ⋅ p^tk~n~^ = p^ntk^
Full compartmentalization reduces n to 1, leaving us with a function of time only p^tk^. ∎
Theorem: While it is possible that there exist past or present conspiracies w.h.p. of never being exposed:
Proof: The lemma holds with the following catch.
(P1) p^tk^ is still exponential over time t unless the sole conspirator, upon setting a plot in motion w.p. p^t~1~k^ = p^k^, is eliminated from the function such that p^k^ is the final (constant) probability.
(P2) For n = 1, this is really more a plot by an individual rather than a proper “conspiracy,” since no individual conspires with another. ∎