Cool Guides

4647 readers

5 users here now

Rules for Posting Guides on Our Community

1. Defining a Guide Guides are comprehensive reference materials, how-tos, or comparison tables. A guide must be well-organized both in content and layout. Information should be easily accessible without unnecessary navigation. Guides can include flowcharts, step-by-step instructions, or visual references that compare different elements side by side.

2. Infographic Guidelines Infographics are permitted if they are educational and informative. They should aim to convey complex information visually and clearly. However, infographics that primarily serve as visual essays without structured guidance will be subject to removal.

3. Grey Area Moderators may use discretion when deciding to remove posts. If in doubt, message us or use downvotes for content you find inappropriate.

4. Source Attribution If you know the original source of a guide, share it in the comments to credit the creators.

5. Diverse Content To keep our community engaging, avoid saturating the feed with similar topics. Excessive posts on a single topic may be moderated to maintain diversity.

6. Verify in Comments Always check the comments for additional insights or corrections. Moderators rely on community expertise for accuracy.

Community Guidelines

Direct Image Links Only Only direct links to .png, .jpg, and .jpeg image formats are permitted.
Educational Infographics Only Infographics must aim to educate and inform with structured content. Purely narrative or non-informative infographics may be removed.
Serious Guides Only Nonserious or comedy-based guides will be removed.
No Harmful Content Guides promoting dangerous or harmful activities/materials will be removed. This includes content intended to cause harm to others.

By following these rules, we can maintain a diverse and informative community. If you have any questions or concerns, feel free to reach out to the moderators. Thank you for contributing responsibly!

founded 1 year ago

MODERATORS

[email protected]

345

US Majors With The Highest Unemployment/UnderEmployment Rates (lemmy.today)

submitted 6 months ago by [email protected] to c/[email protected]

98 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

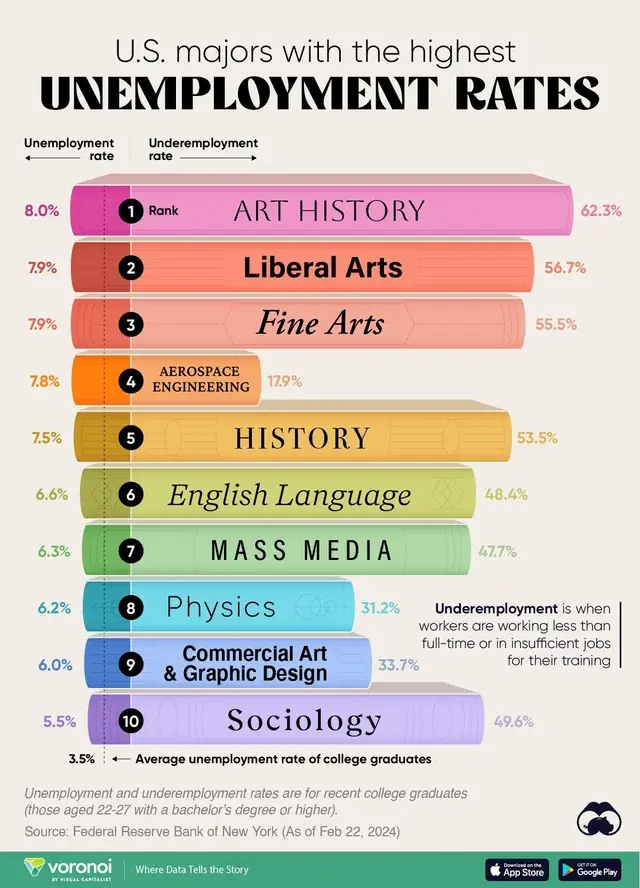
[–] [email protected] 16 points 6 months ago (1 children)

I double majored in History of Art and Philosophy for my undergrad.

Surprisingly philosophy led on quite neatly to a career in software development. Especially analytic philosophy is all about breaking down complex problems into premises and a conclusion. Sometimes it's algorithmic in the sense that premise 4 might refer you back to premise 2.

[–] [email protected] 6 points 6 months ago (1 children)

That's super interesting to me, any references for a software person who wants to find some overlap with philosophy? I know very little about the subject.

[–] [email protected] 7 points 6 months ago (1 children)

I suppose studying basic formal logic would be a good place to start because that is the place where there is the most overlap. In philosophy an argument can be 'valid' by conforming to certain conditions such as

P1: All men are mortal
P2: Socrates is a man
C: Socrates is mortal

This is an example of deductive reasoning where the form or structure of the argument guarantees the conclusion to be true. Process is called 'deductive' reasoning where a conclusion is drawn from the truth of the premises. The ancient Greeks called this a syllogism.

Computer programs are similar in the sense that they are using formal logic with tokens that represent variables to the compiler. Given these arguments exist; we can perform these operations and get a specific result.

As an aside the counterpart to deductive reasoning is inductive reasoning. That's where the premises may be true but the conclusion might not necessarily follow from them. People throw around the word 'fallacy' quite often online but essentially every fallacy is just an example of inductive reasoning where the premises do not guarantee the conclusion. Philosophers study different types of formal fallacies like 'post hoc ergo propter hoc' (because this happens, something else ought to happen) since there are different ways where combinations of premises can lead to an untrustworthy conclusion.

Intriguingly all science is speculative and uses inductive reasoning where we infer from what data we gain in experiments to a conclusion of what might be happening, however there is no logical guarantee that experiment results will be true. There's even a thesis called pessimistic meta induction which states that: Given all scientific theories we held in the past have been proven false (or refined to a slightly different conclusion), we can safely assume that every scientific theory we currently hold is 'false' in some sense.

[–] [email protected] 4 points 6 months ago

This is a good introduction to formal logic. It was required reading in my undergrad - https://emilkirkegaard.dk/en/wp-content/uploads/Paul-Tomassi-Logic.pdf