It's about asking, "how does this algorithm behave when the number of elements is significantly large compared to when the number of elements is orders of magnitude larger?"
Big O notation is useless for smaller sets of data. Sometimes it's worse than useless, it's misguiding. This is because Big O is only an estimate of asymptotic behavior. An algorithm that is O(n^2) can be faster than one that's O(n log n) for smaller sets of data (which contradicts the table below) if the O(n log n) algorithm has significant computational overhead and doesn't start behaving as estimated by its Big O classification until after that overhead is consumed.
#computerscience
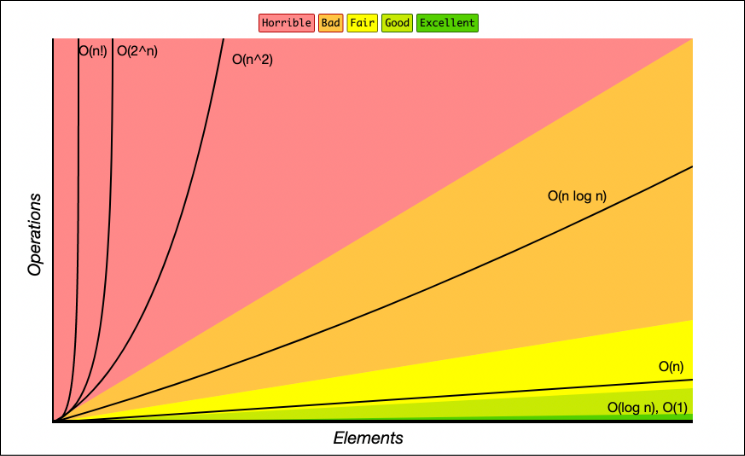
Image Alt Text:
"A graph of Big O notation time complexity functions with Number of Elements on the x-axis and Operations(Time) on the y-axis.
Lines on the graph represent Big O functions which are are overplayed onto color coded regions where colors represent quality from Excellent to Horrible
Functions on the graph:
O(1): constant - Excellent/Best - Green
O(log n): logarithmic - Good/Excellent - Green
O(n): linear time - Fair - Yellow
O(n * log n): log linear - Bad - Orange
O(n^2): quadratic - Horrible - Red
O(n^3): cubic - Horrible (Not shown)
O(2^n): exponential - Horrible - Red
O(n!): factorial - Horrible/Worst - Red"
Source
I mean...yeah. Just because something is provably the best possible thing, doesn't mean it's good. Sorting should be avoided if at all possible. (And in many cases, such as with numbers, you can do better than comparison-based sorts)