this post was submitted on 17 Aug 2023
156 points (100.0% liked)
Math Memes
1530 readers
2 users here now
Memes related to mathematics.
Rules:
1: Memes must be related to mathematics in some way.
2: No bigotry of any kind.
founded 1 year ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
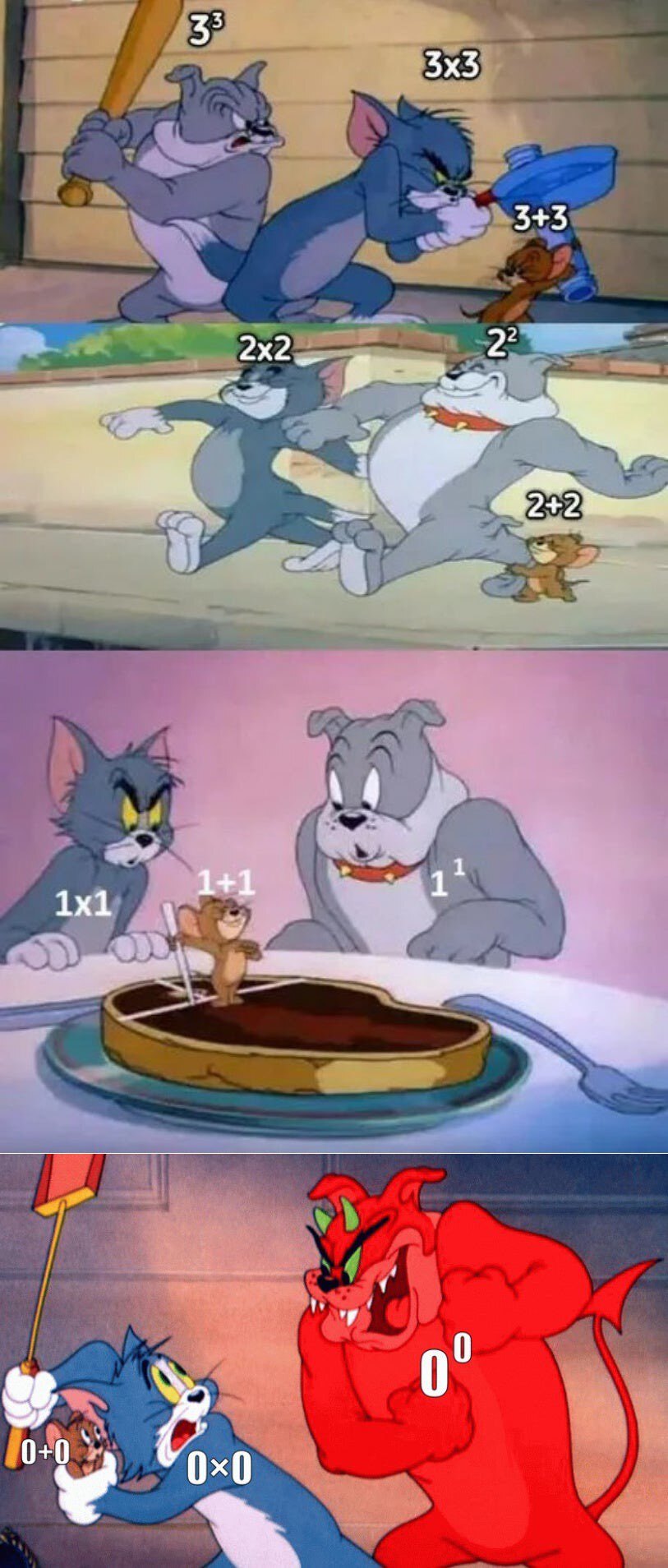
it makes graphs look nicer.
however, 0^0 isn't 0x0, that would be 0^2. 0^1 is 0x1, anything^0 is... well, it's 1. afaik there isn't am equivalent mathematical expression to n^0, it's multiplying a number by itself -1x, or something equally mind melting.
actually, I thought of a (maybe) helpful way to visualise this.
x^-n is equivalent to 1÷(x^n), so 10^-1 is one tenth, 10^-2 is one hundredth, so on. the number, x, appears in the equation n times.
you can view positive exponents as the inverse, (x^n)÷1. likewise, the number appears n times.
so what happens for x^0? well, zero is neither positive nor negative. and to maintain consistency, x must appear in the equation zero times. so what you're left with is 1÷1, regardless of what number you input as x.
I'd imagine you want something defined recursively like multiplication
So it needs to be
On an unrelated note, it'd be nice if Lemmy had Mathjax. I just wrote all this on mobile with that assumption, and I'm not rewriting now that I know better.
Indeed, my mind is melted.