Map Enthusiasts

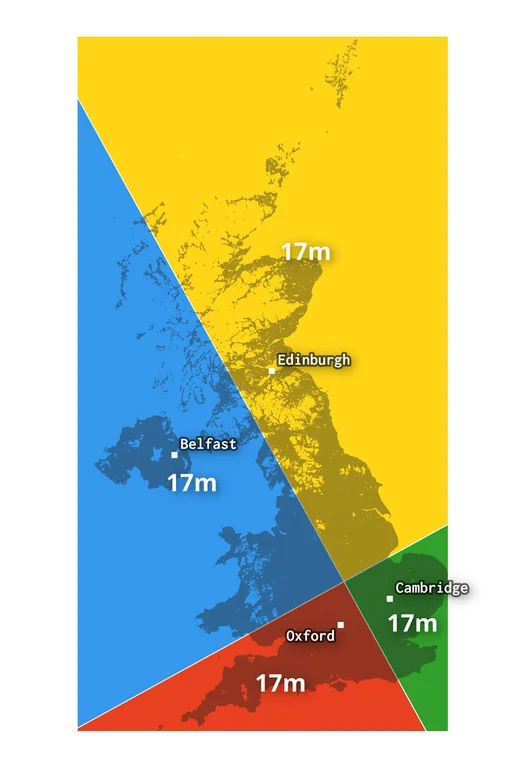
I think it might not be possible.

Imagine the population is a uniform circle centred around that intersection point so the quadrants have equal population - but make the circle small enough it doesn't reach Belfast.

Now add one person in Belfast. How do we move the lines slightly so it's still right?

If you move NNW along the line, Belfast quadrant can match Oxford and Cambridge, but Edinburgh is too small. If you move WSW, Edinburgh, Cambridge and Belfast quadrants match but Oxford is too small.

If you move the intersection point directly toward Belfast, does that work? I think Cambridge quadrant grows faster than either Edinburgh or Oxford.

You can rotate it first. Not a tiny amount but all the way round to make one line go through Belfast's new resident. Then move the intersection slightly.

So that means, for a tiny change (continuous variation) in the population distribution, the supposed intersection and/or angle are discontinuous (sudden big change). That discontinuity ruins my approaches to finding a proof, and I think means there might not be one. It might not always be possible to get perpendicular equal quadrants like that.

That's as far as I got, anyway!