Pull the switch as the trolley is on that rail so it gets stuck and the trolley kills nobody
this post was submitted on 27 Feb 2024
946 points (97.6% liked)
Science Memes
14207 readers
2467 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.
Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- !abiogenesis@mander.xyz
- !animal-behavior@mander.xyz
- !anthropology@mander.xyz
- !arachnology@mander.xyz
- !balconygardening@slrpnk.net
- !biodiversity@mander.xyz
- !biology@mander.xyz
- !biophysics@mander.xyz
- !botany@mander.xyz
- !ecology@mander.xyz
- !entomology@mander.xyz
- !fermentation@mander.xyz
- !herpetology@mander.xyz
- !houseplants@mander.xyz
- !medicine@mander.xyz
- !microscopy@mander.xyz
- !mycology@mander.xyz
- !nudibranchs@mander.xyz
- !nutrition@mander.xyz
- !palaeoecology@mander.xyz
- !palaeontology@mander.xyz
- !photosynthesis@mander.xyz
- !plantid@mander.xyz
- !plants@mander.xyz
- !reptiles and amphibians@mander.xyz
Physical Sciences
- !astronomy@mander.xyz
- !chemistry@mander.xyz
- !earthscience@mander.xyz
- !geography@mander.xyz
- !geospatial@mander.xyz
- !nuclear@mander.xyz
- !physics@mander.xyz
- !quantum-computing@mander.xyz
- !spectroscopy@mander.xyz
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and sports-science@mander.xyz
- !gardening@mander.xyz
- !self sufficiency@mander.xyz
- !soilscience@slrpnk.net
- !terrariums@mander.xyz
- !timelapse@mander.xyz
Memes
Miscellaneous
founded 2 years ago
MODERATORS
Yes. Right under trolley. Will derail it.
@tedu @science_memes @fossilesque Can we space them out so the frequency is the same? 😂
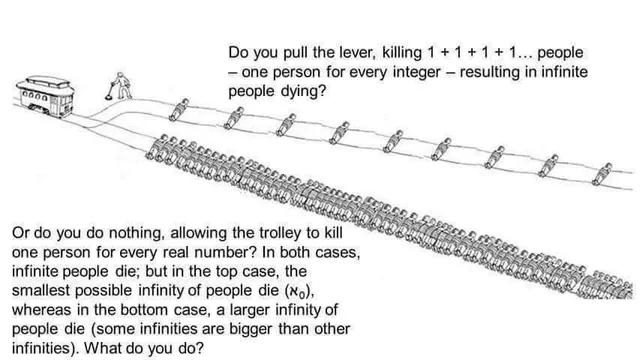
Was this an honest question? Because the answer is 'no'. You can't space them out or else the set of people on the lower track would be countable which is a smaller infinity than the ones of the real numbers.
To space them, you would have to take people of the track. Infinitely many. To be precise not all of them but as many as there are on the track.
Multi-track drifting. Also while some infinities are smaller if you're just counting out an infinite number of individual humans then I'm pretty sure they're the same size infinities one is just social distancing. Smaller infinities are ones like those in between each part of the bigger infinities. To represent a smaller infinity you'd maybe have to have an infinite number of smaller humans crammed into a spot the size of one of the spaces between the humans on the other track, or something along those lines. The real number track does contain smaller infinities between each integer via infinite decimal points but I don't think one track would technically be smaller than the other in this case since they run parallel to each other but neither are technically limited in the "length" of their infinity so to speak. But I could be misremembering how they classify smaller infinities.
Infinity cannot be divided, if it can then it becomes multiple finite objects. Therefore there cannot be multiple Infinities. If infinity has a size, then it is a finite object. If infinity has a boundary of any kind, then it is a finite object.
Infinity cannot be divided, if it can then it becomes multiple finite objects.
It really depends on what you mean by infinity and division here. The ordinals admit some weaker forms of the division algorithm within ordinal arithmetic (in particular note the part about left division in the link). In fact, even the cardinals have a form of trivial division.
Additionally, infinite sets can often be divided into set theoretic unions of infinite sets fairly easily. For example, the integers (an infinite set) is the union of the set of all integers less than 0 with the set of all integers greater than or equal to 0 (both of these sets are of course infinite). Even in the reals you can divide an arbitrary interval (which is an infinite set in the cardinality sense) into two infinite sets. For example [0,1]=[0,1/2]U[1/2,1].
Therefore there cannot be multiple Infinities.
In the cardinality sense this is objectively untrue by Cantor's theorem or by considering Cantor's diagonal argument.
Edit: Realized the other commenter pointed out the diagonal argument to you very nicely also. Sorry for retreading the same stuff here.
Within other areas of math we occasionally deal positive and negative infinities that are distinct in certain extensions of the real numbers also.
If infinity has a size, then it is a finite object.
Again, this is not really true with cardinals as cardinals are in some sense a way to assign sizes to sets.
If you mean in terms of senses of distances between points, in the previous link involving the extended reals, there is a section pointing out that the extended reals are metrizable, informally this means we can define a function (called a metric) that measures distances between points in the extended reals that works roughly as we'd expect (such a function is necessarily well defined if either one or both points are positive or negative infinity).
If infinity can be measured, by either size, shape, distance, timespan or lifecycle, then the object being considered infinite is a finite object. Infinity, nothing, and everything follow these same rules. If there are two multiple infinite objects side by side to each other, which means there is a measurable boundry that seperates them, then those objects aren't infinite, they are finite objects, within an infinite space that contains them. Only the space that contains these objects is infinite. Any infinite numbers that are generated within this infinite space, regardless of where they originated within this space, belong to this single infinity. There is no infinityA or infinityB there is just infinity itself.
My degree is in math. I feel pretty confident in saying that you are tossing around a whole bunch of words without actually knowing what they mean in a mathematical context.
If you disagree, try the following:
-
What is a function? What is an injective function? What is a surjective function? What is a bijection?
-
In mathematics, what does it mean for a set to be finite?
-
In mathematics, what does it mean for a set to be infinite?
I'm willing to continue this conversation if you can explain to me in reasonably rigorous terms what those words mean. I'll help you do it too. The link I sent you in my previous post that mentions cardinal numbers links you to a wikipedia page that links to articles explaining what finite and infinite sets are in the first paragraph.
To be clear here, your answer for 2 specifically should rely on your answer from 1 as the mathematical definition of a finite set is in terms of functions and bijections.
Here are some bonus questions for you to try also:
-
In mathematics, what does it mean for a set to be countable?
-
In mathematics, what does it mean for a set to be uncountable?
A finite universe, the one in which we live, can only produce finite objects. Those finite objects can only produce other finite objects. A finite object cannot create an infinite object, as the act of creation would be a starting point for the object, and if an object has a starting point or an end point, which are really the same thing, then the object is a finite object.
If a set of numbers originates from a starting point and moves away from that point in a seemingly infinite distance, and then you decide to traverse that set in the opposite direction towards the starting point, the starting point becomes an ending point, and if an object, in this case the set itself, has an ending point, it is a finite object. Finite objects cannot create infinite objects because the act of creation would negate their infinity. Infinity is neither created nor ends, nor does it have size, shape, or form.
None of this includes the correct answers to the questions I asked you. I'm not going to read anything else from you until you correctly answer the questions I asked.
load more comments
(8 replies)
load more comments
(3 replies)