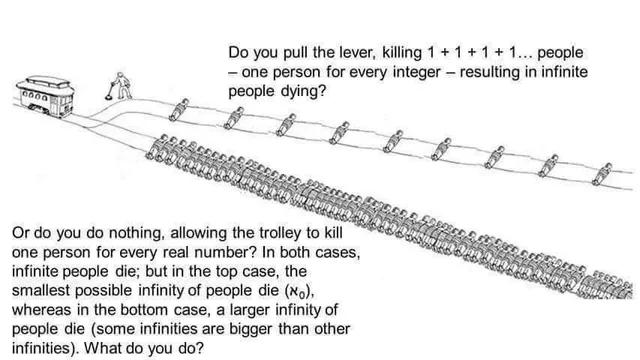
Did nobody have math class? The pictures are always misleading!

It never actually specifies the density the people are packed onto the track, the image implies an answer.

I'd argue that the densities should be considered to be equal, regardless of whatever that density value may be. We do not need to solve for the exact value to discuss the problem at hand!

Would suck being the last person on either track. It'd be a long and boring wait while tied up

Jump in front of the trolley, someone else's problem

This comment section is politics in action! :-P

Invent a new number system that provides aneven smaller infinity

I know many people despise generative AI, but what do you think of this result from Copilot? I am bad at maths so I wonder if you experts can tell.

In your scenario, you have two sets: the integers on the top track and the real numbers on the bottom track. The cardinality of the integers is equal to the cardinality of the real numbers, which is called the continuum hypothesis. Therefore, it seems intuitively more ethical to pull the lever and divert the trolley to the bottom track, where you kill fewer people in any finite time.

i'd ask for a second train.

I get that the answer is supposed to be "it doesn't matter" but if you take time into account, it actually fucking does, and also makes it hugely obvious what the actual answer is.

If we have infinite people, it wouldn't be such a bad thing to lose a couple.

Some infinities are bigger than others but those are both the same sized infinity, ℵ₀. Same if you multi-track drift.

Edit: I didn't read it closely enough, it says "one person for every real number". Which is indeed a larger infinity. However I don't think you can diagram that, the diagram is showing a countable infinity of people on the lower track.

Killing one person for each real number, the train will be killing an uncountably infinite quantity of people in any given finite time slice.

Pull the lever. Save as many lives as you can and hope that someone that now wasn't killed as fast can help come up with a solution for the runaway trolley.

EDIT: I rolled a critical fail in reading comprehension and I thought the other track was N per integer instead of 1 per real number in the previous version of this comment.

The people in the real number track are already dead by the time the trolley arrives due to the forces involved in cramming them so tightly together. I.e. they are basically just a gore pile the moment after the people are somehow arranged like that.

I pick the real number track so that no one new has to die.

If the tracks are scaled to the same unit (presumably one where one human width equals an infinitely small number), everyone in the top track would die of exposure before the trolley even reaches its first victim due to there being infinite distance between integer milestones, whereas everyone in the bottom track would be killed instantly due to any distance traveled having an infinite number of infinitesimals*. So I choose the bottom track to be merciful.

If the tracks don't share the same scale then we don't have enough information to make a judgment.

* Even though we already established the one human width rule. Could someone check my logic here? Infinities break my brain.

I'll do nothing. Either way those people will eventually die - because of the train or because of starvation and dehydration. I would prefer the train.

Infinity people always die. Even if you don't make a decision.

I pull the lever and invoke Zeno's paradox to ensure the trolley's position remains < 1 for eternity.

I am sure even countably infinite people would violate some law of thermodynamics.

Pull it -1/12 of the way, causing the infinity to converge to a real number.